Advanced Human Activity Clustering
This script extends the example from ClusterAnalysis.m to evaluate other clustering methods. In particular, it addresses: * Hierarchical Clustering, Dendrograms & Cophenetic Correlation * Fuzzy C-means Clustering (Fuzzy Logic Toolbox) * Self-Organizing Maps (Neural Network Toolbox) * Evaluating & Comparing Clustering Solutions
The dataset is courtesy: Davide Anguita, Alessandro Ghio, Luca Oneto, Xavier Parra and Jorge L. Reyes-Ortiz. Human Activity Recognition on Smartphones using a Multiclass Hardware-Friendly Support Vector Machine. International Workshop of Ambient Assisted Living (IWAAL 2012). Vitoria-Gasteiz, Spain. Dec 2012
Contents
Load Data
Load Human-Activity dataset for clustering.
load Data\HAData Xtrain features % Perform PCA decomposition [coeff,score,latent] = pca(Xtrain);
Initial Clustering Solution Baseline
Compute initial K-means clustering solution for comparison
rng(1) kidx = kmeans(Xtrain, 3, 'distance', 'correlation', 'replicates', 5);
Hierarchical Clustering, Cophenetic Corr. Coeff. and Dendrogram
Hierarchical Clustering groups data over a variety of scales by creating a cluster tree or dendrogram. The tree is not a single set of clusters, but rather a multilevel hierarchy, where clusters at one level are joined as clusters at the next level. A variety of distance measures such as Euclidean, Mahalanobis, Jaccard etc. are available.
Cophenetic correlation coefficient is typically used to evaluate which type of hierarchical clustering is more suitable for a particular type of data. It is a measure of how faithfully the tree represents the similarities/dissimilarities among observations.
Dendrogram is a graphical representation of the cluster tree created by hierarchical clustering.
Z = linkage(score(:,1:8), 'ward'); hidx = cluster(Z, 'maxclust', 3); pairscatter(score(:,1:4), [], hidx)
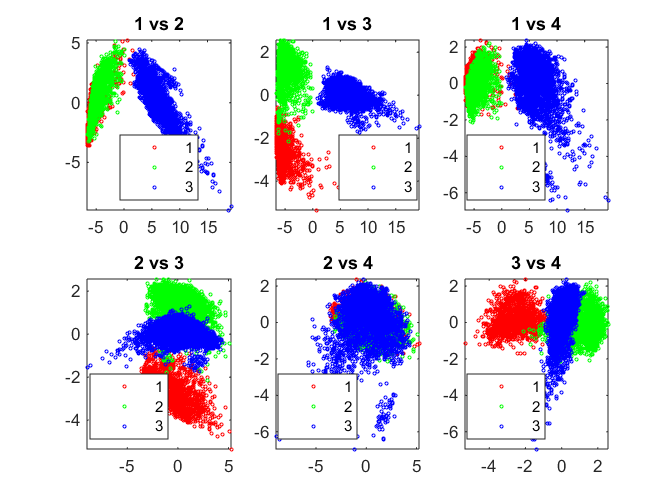
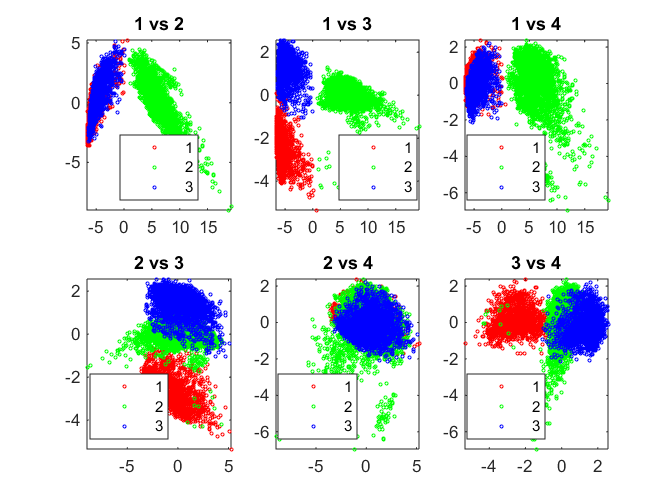
Fuzzy C-Means
Fuzzy C-means (FCM) is a data clustering technique wherein each data point belongs to a cluster to some degree that is specified by a membership grade. The function fcm returns a list of cluster centers and several membership grades for each data point.
fcm iteratively minimizes the sum of distances of each data point to its cluster center weighted by that data point's membership grade.
[center,U] = fcm(score(:,1:8), 3);
% Generate hard clustering for evaluation
[~, fidx] = max(U);
fidx = fidx';
pairscatter(score(:,1:4), [], fidx)
Iteration count = 1, obj. fcn = 137819.579437 Iteration count = 2, obj. fcn = 107281.114182 Iteration count = 3, obj. fcn = 106944.221021 Iteration count = 4, obj. fcn = 103944.473308 Iteration count = 5, obj. fcn = 85623.085511 Iteration count = 6, obj. fcn = 60847.812140 Iteration count = 7, obj. fcn = 57132.202217 Iteration count = 8, obj. fcn = 56342.025480 Iteration count = 9, obj. fcn = 55881.538183 Iteration count = 10, obj. fcn = 55379.297388 Iteration count = 11, obj. fcn = 54930.558578 Iteration count = 12, obj. fcn = 54645.521084 Iteration count = 13, obj. fcn = 54504.706074 Iteration count = 14, obj. fcn = 54440.348551 Iteration count = 15, obj. fcn = 54406.185557 Iteration count = 16, obj. fcn = 54380.022611 Iteration count = 17, obj. fcn = 54351.219593 Iteration count = 18, obj. fcn = 54313.047763 Iteration count = 19, obj. fcn = 54259.596197 Iteration count = 20, obj. fcn = 54185.188121 Iteration count = 21, obj. fcn = 54085.785091 Iteration count = 22, obj. fcn = 53962.397562 Iteration count = 23, obj. fcn = 53824.908242 Iteration count = 24, obj. fcn = 53691.594492 Iteration count = 25, obj. fcn = 53580.954715 Iteration count = 26, obj. fcn = 53501.834614 Iteration count = 27, obj. fcn = 53451.711405 Iteration count = 28, obj. fcn = 53422.533283 Iteration count = 29, obj. fcn = 53406.404596 Iteration count = 30, obj. fcn = 53397.740578 Iteration count = 31, obj. fcn = 53393.154589 Iteration count = 32, obj. fcn = 53390.744938 Iteration count = 33, obj. fcn = 53389.483464 Iteration count = 34, obj. fcn = 53388.824343 Iteration count = 35, obj. fcn = 53388.480329 Iteration count = 36, obj. fcn = 53388.300904 Iteration count = 37, obj. fcn = 53388.207367 Iteration count = 38, obj. fcn = 53388.158622 Iteration count = 39, obj. fcn = 53388.133225 Iteration count = 40, obj. fcn = 53388.119996 Iteration count = 41, obj. fcn = 53388.113106 Iteration count = 42, obj. fcn = 53388.109518 Iteration count = 43, obj. fcn = 53388.107650 Iteration count = 44, obj. fcn = 53388.106677 Iteration count = 45, obj. fcn = 53388.106171 Iteration count = 46, obj. fcn = 53388.105907 Iteration count = 47, obj. fcn = 53388.105770 Iteration count = 48, obj. fcn = 53388.105698 Iteration count = 49, obj. fcn = 53388.105661 Iteration count = 50, obj. fcn = 53388.105642 Iteration count = 51, obj. fcn = 53388.105631 Iteration count = 52, obj. fcn = 53388.105626
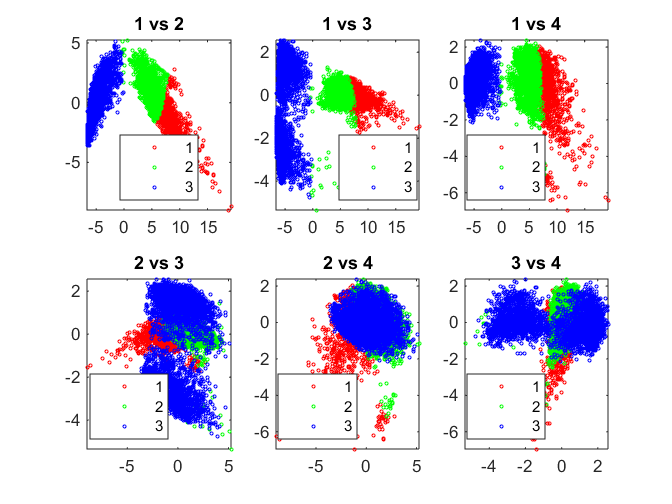
Neural Networks - Self Organizing Maps (SOMs)
Neural Network Toolbox supports unsupervised learning with self-organizing maps (SOMs) and competitive layers.
SOMs learn to classify input vectors according to how they are grouped in the input space. SOMs learn both the distribution and topology of the input vectors they are trained on. One can make use of the interactive tools to setup, train and test a neural network. It is then possible to auto-generate the code for the purpose of automation. The code in this section has been auto-generated.
% Create a Self-Organizing Map dimension1 = 3; dimension2 = 1; net = selforgmap([dimension1 dimension2]); % Train the Network net.trainParam.showWindow = 1; [net,tr] = train(net, Xtrain'); % Test the Network nidx = net(Xtrain'); nidx = vec2ind(nidx)'; % Visualize results pairscatter(score(:,1:4),[],nidx);
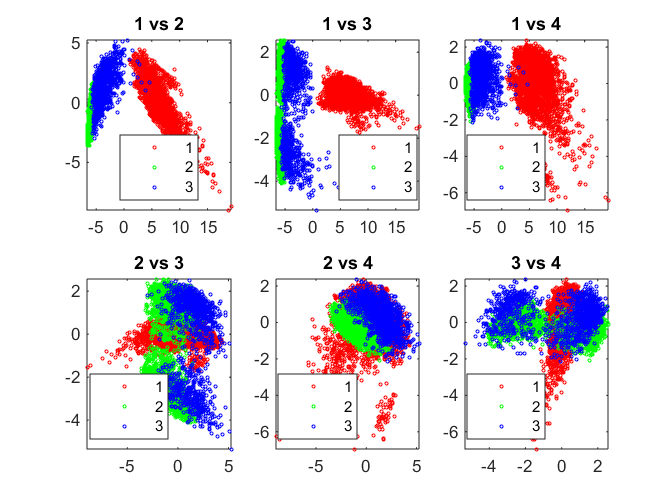
Gaussian Mixture Models (GMM)
Gaussian mixture models are formed by combining multivariate normal density components. gmdistribution.fit uses expectation maximization (EM) algorithm, which assigns posterior probabilities to each component density with respect to each observation. The posterior probabilities for each point indicate that each data point has some probability of belonging to each cluster.
gmobj = fitgmdist(score(:,1:8), 3, 'Replicates', 5);
gidx = cluster(gmobj, score(:,1:8));
pairscatter(score(:,1:4), [], gidx);
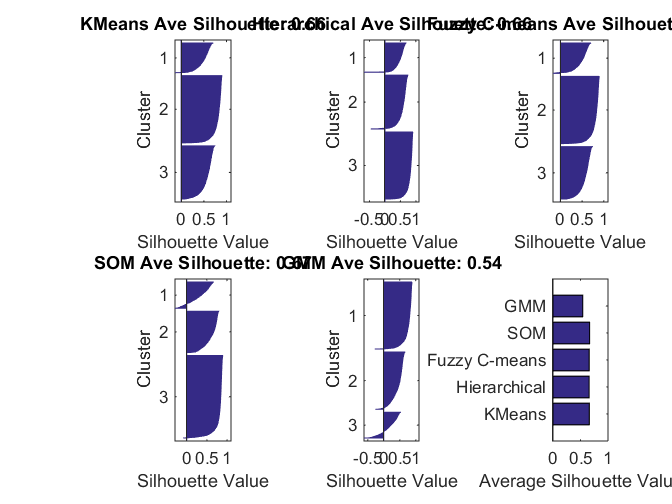
Cluster Evaluation
Compare clustering solutions using average silhouette value. This is one objective criterion. It may not guarantee the best clustering solution, which can be a subjective determination.
sols = [kidx hidx fidx nidx gidx];
methods = {'KMeans','Hierarchical','Fuzzy C-means','SOM','GMM'};
silAve = zeros(1, size(sols,2));
for i = 1:size(sols,2)
subplot(2,3,i);
%[silh,~] = silhouette(Xtrain, sols(:,i), 'correlation');
[silh,~] = silhouette(score(:,1:8), sols(:,i));
silAve(i) = mean(silh);
title(sprintf('%s Ave Silhouette: %0.2f', methods{i}, silAve(i)));
end
subplot(2,3,6);
barh(silAve); xlabel('Average Silhouette Value');
set(gca,'YTick', 1:length(silAve), 'YTickLabel', methods);
Determining Number of Clusters
The evalclusters function can be used to evaluate a clustering algorithm like kmeans for different number of clusters and calculate a metric that can be used to determine the optimal number of clusters.
Notice that here, for both kmeans and hierarchical clustering, the optimal number of clusters is 2.
ev1 = evalclusters(score(:,1:8),'kmeans','CalinskiHarabasz','KList',2:6) ev2 = evalclusters(score(:,1:6),'kmeans','DaviesBouldin','KList',2:6) ev1 = evalclusters(score(:,1:8),'linkage','CalinskiHarabasz','KList',2:6) ev2 = evalclusters(score(:,1:6),'linkage','DaviesBouldin','KList',2:6)
ev1 =
CalinskiHarabaszEvaluation with properties:
NumObservations: 7352
InspectedK: [2 3 4 5 6]
CriterionValues: [1.9534e+04 1.2766e+04 1.1405e+04 9.9601e+03 8.9938e+03]
OptimalK: 2
ev2 =
DaviesBouldinEvaluation with properties:
NumObservations: 7352
InspectedK: [2 3 4 5 6]
CriterionValues: [0.5312 0.9129 1.1035 1.0865 1.1257]
OptimalK: 2
ev1 =
CalinskiHarabaszEvaluation with properties:
NumObservations: 7352
InspectedK: [2 3 4 5 6]
CriterionValues: [1.9403e+04 1.2426e+04 1.0694e+04 9.0625e+03 8.0660e+03]
OptimalK: 2
ev2 =
DaviesBouldinEvaluation with properties:
NumObservations: 7352
InspectedK: [2 3 4 5 6]
CriterionValues: [0.5323 0.9626 1.1654 1.0866 1.1405]
OptimalK: 2